¿QUE ES UNA INTEGRAL?

 Proceso que permite restituir una función que ha sido previamente derivada. Es decir, la operación opuesta de la derivada así como la suma es a la resta.

Por conveniencia se introduce  una notación para la antiderivada de una función

Si F(x) = f(x),  se representa 

∫f x  dx=F(x) + c

A este grafo ∫ se le llama símbolo de  la integral y a la notación ∫f (x)  dx se le llama integral indefinida  de f(x) con respecto a x. La función f(x) se denomina integrando, el proceso recibe el nombre de integración. Al número C se le llama    conste de integración esta surge por la imposibilidad  de la constante derivada. Así como dx denota diferenciación son respecto a la variable x, lo cual indica la variable derivada.

∫f (x)dx

Esto se lee integral de f de x del diferencial de x

Propiedades

·          ∫  k[f(x)] dx = k ∫f (x)  dx

·         ∫ [f (x)+ g(x)]  dx = ∫f (x) dx + ∫g (x) dx

K=ES UNA CONSTANTE

FORMULARIO DE INTEGRABLES INMEDIATAS

INTEGRALES DE FUNCIONES

-       Integrales inmediatas.

Se llaman integrales inmediatas aquellas que están en la tabla de integrales, su solución es inmediata pues se trata sólo de poner el resultado que aparece en la tabla (son las mas sencillas y las que debes de ejercitar).

Ejemplo 1: Hallemos la integral

En ocasiones una integral es inmediata, aunque a algunos no les parezca en principio.

En esta se aplicó la fórmula:

  Ejemplo 2: Hallemos la integral

Y aplicamos nuevamente la formula anterior.

Ejemplo 4: Hallemos la integral





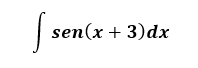
Solución:
Hacemos (x + 5) = u, y diferenciando los dos miembros de la igualdad: dx=du. A continuación sustituimos:

-         Integración por descomposición.

 Se trata de aprovechar la propiedad de linealidad:

De esta manera, siempre que podamos descomponer una integral en varios sumandos lo haremos así. 

 Ejemplo 4: Hallemos la integral

 Solución: Esta integral puede ser descompuesta en sumandos más simples,

-         Integrales por sustitución o cambio de variable

Basado en la expresión:

o expresado de otra manera:

se trata de hacer una sustitución: g(x) = t, a continuación diferenciando la igualdad:

g' (x) dx = dt

Para convertir la integral de x en otra integral de t que sea inmediata, o por lo menos más sencilla de integrar.
Ejemplo 5: Hallemos la integral  

Solución: Podemos observar que cos x es la derivada de sen x, por lo que la sustitución adecuada es:  t = sen x, a continuación diferenciamos ambos miembros y:  dt = cos x dx, entonces:

  Ejemplo 6: Hallemos la integral

  Solución: Podemos observar que 1/x es la derivada de ln x, por tanto la sustitución es ln x = t, y diferenciando tenemos dx/x = dt :

 Ejemplo 7: Hallemos la integral 

  Solución: La sustitución adecuada es:

 Ejemplo 8: Hallemos la integral

 Solución: Podemos observar que la derivada del denominador es (1 + x²)' = 2 x, entonces en la integral podemos multiplicar y dividir por 2:

y ahora hacemos la sustitución: 1 + x² = t ,  2x dx = dt. O sea,

 Ejercicios para el alumno:

METODOS DE INTEGRACION

      

Integración de funciones racionales mediante fracciones parciales:

R(x) = Q(x)/P(x)

Caso 1. Las raíces del polinomio del denominador son reales y distintas entre sí, es decir;

P(X) = (x-a) (x-b)…… (x-d)

∫ R(x) dx =   ∫ [Q(x)/P(x)] dx =   ∫ A/(x-a) dx + ∫ B/(x-b)……+ ∫ D/(x-d) dx

=A Ln lx-al + B Ln lx-bl…….. + D Ln lx-dl + k

Caso 2. Las raíces del polinomio del denominador son reales, pero algunas son múltiples, es decir;

P(x) = (x-a)˄m (x-b)˄n…… (x-d)˄f

∫ R(x) dx =   ∫ [Q(x)/P(x)] dx =   ∫A1/(x-a) ˄m dx +∫ [A2/(x-a) ˄ (m-1)] dx+…∫ [Am/(x-a)

ᴧ(m)] dx  + ∫  B1/(x-b) ˄n dx + ∫  [B2/(x-b) ˄(n-1)] dx+ ….. ∫  Bn/(x-b) ˄n dx +……

Caso 3. En la descomposición del polinomio del denominador aparece un factor x˄2 + px + q irreducible en el campo de los números reales (no puede factorizarse).

Caso 4. En la descomposición del polinomio del denominador aparece un factor x˄2 + px + q irreducible en el campo de los números reales (no puede factorizarse), elevado a un potencia.

Ejemplo 9. Hallar la siguiente integral

Procedemos a construir las ecuaciones

A+B=0

3A-B+C=1

3A-B+D=0

A-B-C-D=-1

Resolvemos el sistema de ecuaciones y obtenemos

C=1, B=0, D=0,A=0

La integral corresponde:

EJERCICIOS PARA EL ALUMNO

BIBLIOGRAFIA 

Granville, "Cálculo diferencial e Integral". Limusa, Trillas.

POR FAVOR UN LIKE A MI PAGINA DE FACEBOOK¡¡¡
https://www.facebook.com/asesoriasmejoradas

Y RECUERDA SI TIENES ALGUNA DUDA CON LOS EJERCICIOS YO TE AYUDO, YA SEA POR TU COMENTARIO O POR MI PAGINA DE FACEBOOK QUE TE RESPONDERÉ CON MAS RAPIDEZ¡¡